3.0 Digital Logic
As
we all known , informations inside a computer is processed and stored as 0-1
bit. Followed by graphical symbol and algebraic expression of basic logic gates such as AND gate , OR gate , NOT gate and also universal gates , NAND gate , NOR gate and XOR gate. These gates sometimes act as a switch also.
3.1 basic logic gates
AND gate

The notation for the AND of A and B is A*B or AB
A.B =Y
truth table:
A
|
B
|
Y=A.B
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
OR
gate
The
notation for the OR of A and B is A+B
A+B=Y
truth table:
A
|
B
|
Y=A+B
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
NOT gate
The notation
for the COMPLEMENT or NOT of A is A'
A=A'
truth table :
A
|
A'
|
0
|
0
|
1
|
0
|
NAND gate
The term “NAND” stands for “not-and” meaning that output C
is the inverse from the AND gate
A.B=(A.B)’=Y
truth table:
| A |
B
|
Y=(AB)’
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
NOR gate
The term “NOR” stands for “not-or,” meaning that output C is the inverse from the OR gate
A+B=(A+B)’=Y
truth table :
A
|
B
|
Y=(A+B)'
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
3.2 Combinational circuit
Combinational circuit involves circuit that combined gates in altering inputs into various output to suit the circuit builds.
- computes output based on current input and it is a logic block that contains no memory
- it can be defined in three ways
e.g:
A
|
B
|
Y=(A+B)'
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
2.by using graphical symbol
e.g:
3.and using boolean equations
e.g: F=(A.B)+(A+C)'(CB)
3.2.1 Boolean equation form
Boolean equation can be represented in two forms, Sum-Of-Product and Product-Of-Sum.
Sum-of-product (SOP)
- Sum of each product
- Easier to derive from truth table
- E = ((A.B) + (A.C) + (B.C))
Product-of-sum (POS)
- Product each sum.
- Usually used if more 1s produced in output function
- E = ((A+B).(A+C).(B+C))
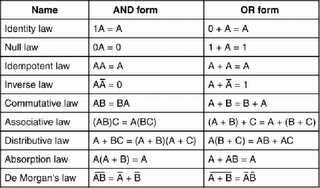
*two ways to simplify boolean equations by using Laws Of Boolean Algebra and De Morgan's Law.
3.2.1.1 Laws Of Boolean Algebra
basic laws of Boolean Algebra
3.2.1.2 De Morgan's Law
first and second De Morgan's Law